Day 11 - Tackling picoCTF's Easy Crypto Challenges

After getting a good feel for the basics on CryptoHack, I decided to switch things up today and test my skills on another popular Capture The Flag (CTF) platform: picoCTF. It's known for being beginner-friendly, and I jumped right into their "Easy Cryptography" challenges to see how the theory I've been learning applies in practice.

Here’s a breakdown of the challenges I solved!

1. Mod 26

The first challenge was called "Mod 26," which was a big hint. The description also explicitly mentioned ROT13.

This is a classic Caesar Cipher, where every letter in the plaintext is shifted by 13 places. A cool property of ROT13 is that applying the same shift twice brings you back to the original text. I wrote a Python script to perform the +13 rotation on each character, handling both uppercase and lowercase letters.

After running the script and providing the ciphertext, it revealed the flag. The flag itself was a nice little joke about the cipher's properties.

Flag: picoCTF{next_time_I'll_try_2_rounds_of_rot13_Aphnytiq}

2. The Numbers

This challenge presented an image with a series of numbers and simply asked, "what do they mean?"

This was another classic substitution cipher, this time mapping numbers to letters based on their position in the alphabet (A=1, B=2, etc.). A one-line Python script was enough to solve this one, converting each number n to its corresponding lowercase letter by calculating chr(n+96).

The script first decoded the numbers into the plaintext picoctfthenumbersmason. Then, I formatted it correctly to get the flag. Flag: picoCTF{thenumbersmason}

3. interencdec

This challenge gave me an encoded file named enc_flag. The first step was to figure out the encoding.

1. Identify Encoding: The content of the file was a long string of characters ending in ==, a classic sign of Base64 encoding.
   
   
2. Decode Base64: I first decoded the string from Base64. However, the output was still jumbled text. This meant there was another layer of cryptography
3. Find the Cipher: The jumbled text looked like it might be from a simple substitution cipher. I pasted the decoded text into CyberChef, a powerful online tool for crypto analysis. I used its "ROT13 Brute Force" recipe, which tries every possible Caesar shift from 1 to 25
4. Reveal the Flag: The output for shift 13 (ROT13) revealed the readable flag!

This was a great example of how ciphers can be layered on top of each other. Flag: picoCTF{caesar_d3cr9pt3d_a47c6d69}

4. hashcrack

This challenge required me to connect to a service using netcat. The service then challenged me to "crack" three different hashes in a row.

The hashes were for common, weak passwords, so I didn't need to run a powerful cracker. I used an online hash lookup tool to find the plaintext for each.

• MD5 Hash: The service provided 482c811da5d5b4bc6d497ffa98491e38. The plaintext was password123.
• SHA-1 Hash: The service provided b7a875fc1ea228b9061041b7cec4bd3c52ab3ce. The plaintext was letmein.
• SHA-256 Hash: The service provided 916e8c4f79b25028c9e467f1eb8ee6d6bbddff965f9928310ad38a8d8869. The plaintext was qwerty098.

After successfully providing all three passwords, the server handed over the flag. Flag: picoCTF{UseStrOnG_h0sHEs_&_P@sswDs!_eff9dbe0}

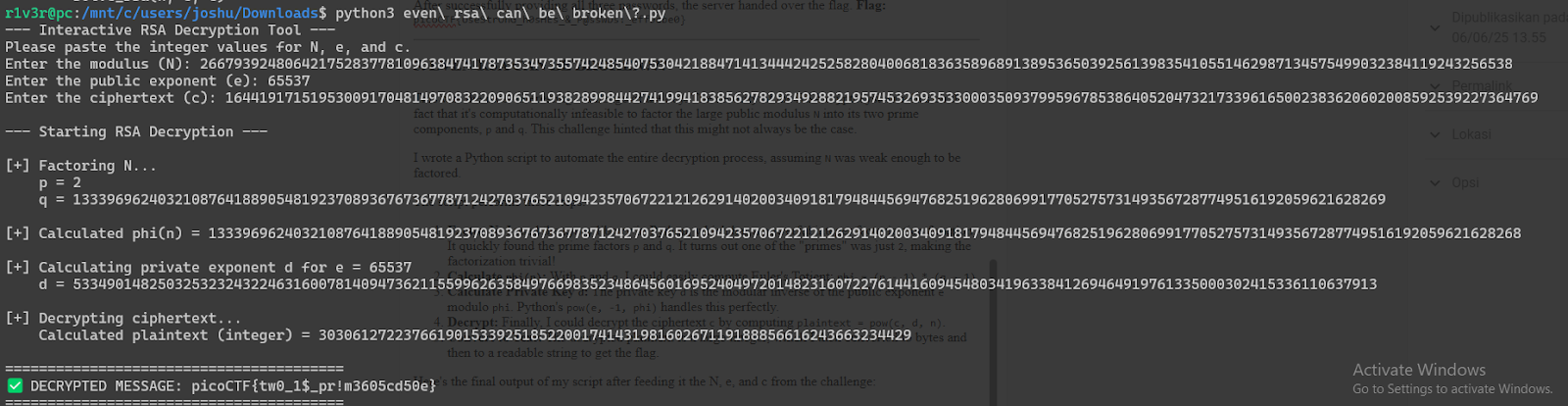
5. EVEN RSA CAN BE BROKEN???

This was the most interesting challenge of the day. The security of the RSA cryptosystem relies on the fact that it's computationally infeasible to factor the large public modulus N into its two prime components, p and q. This challenge hinted that this might not always be the case.

I wrote a Python script to automate the entire decryption process, assuming N was weak enough to be factored.

The script performs these steps:

1. Factor N: I used the sympy library in Python, which has a powerful integer factorization function. It quickly found the prime factors p and q. It turns out one of the "primes" was just 2, making the factorization trivial!
2. Calculate phi(n): With p and q, I could easily compute Euler's Totient: phi = (p - 1) * (q - 1).
3. Calculate Private Key d: The private key d is the modular inverse of the public exponent e modulo phi. Python's pow(e, -1, phi) handles this perfectly.
4. Decrypt: Finally, I could decrypt the ciphertext c by computing plaintext = pow(c, d, n).
5. Convert to Text: The decrypted plaintext is a large integer, which I then converted to bytes and then to a readable string to get the flag.

Here's the final output of my script after feeding it the N, e, and c from the challenge:

Flag: picoCTF{tw0_1$_pr!m3605cd50e}

It was really satisfying to see the RSA steps, which I've been reading about, come together in a practical script to break a "broken" implementation. What a fantastic day of learning at picoCTF!

#IDNBootCampCyber